The numerical implementation of wave-optical (i.e., diffractive) propagation is a large subject. Here in this User Guide, our intent is to specify a few key formulas that outline the concepts and numerical algorithms used by LightLike to propagate optical fields from one transverse plane to another. The discussion here will not fully justify the reasons for choosing one numerical procedure over another, nor will it fully explore the details of the numerical algorthms used in LightLike. What we hope to accomplish in this User Guide discussion is:
(1) To give the user who has some acquaintance with scalar diffraction theory (and its Fourier-transform representations) a clear general idea of which propagator formulas are used in core LightLike propagation modules
(2) To use the knowledge in item (1) to make the user comfortable with the terminology and logic involved in setting mesh and distance parameters in core LightLike propagation modules
(3) To give the user an overview of LightLike's ability to model non-monochromatic versus monochromatic propagation.
One can group LightLike diffractive-propagation modules into two categories:
(1) Fresnel-propagation modules that propagate an optical field from one transverse plane through some arbitrary distance to another transverse plane
(2) Fraunhofer-propagation modules that take an incident optical field, and then propagate to (or perhaps near) the focal plane of an assumed lens.
The most commonly-used modules that set up or perform Fresnel propagation are PropagationController, AtmoPath, and VacuumProp. The PropagationController does not actually carry out any propagations, but it can be used for setting key propagation parameters. AtmoPath is a complicated component that contains phase screen action as well as multiple, sequential Fresnel propagation action. VacuumProp is more basic in the sense that it carries out one propagation over a single specified distance.
The most commonly-used module of the Fraunhofer group is Camera. Another important Fraunhofer-propagation module is HartmannWfsDft, which models a Shack-Hartmann (or plain Hartmann) wavefront sensor.
Theoretical background
Mathematical representation of the optical field
The core LightLike propagation procedures apply directly to scalar, monochromatic, paraxial optical fields. The general mathematical representation of such a field is
(Eq. 1) Y(x,y,z,t) = U(x,y,z)· exp[ i (kz - wt) ]
where k = 2p/l, w = ck, z is the nominal propagation direction, U is complex, and U(...,z) is slowly varying compared to kz. Any LightLike propagator module operates on an input complex field given in some plane z1, of the form
(Eq. 2) U1(x,y) = A1(x,y) · exp[ i·f1(x,y) ]
The output of the propagator module is the corresponding complex field, U2(x,y), in the specified final plane of constant z2. Of course, LightLike actually works only with samples of U1,2 on discrete transverse meshes(x1i,y1j), (x2i,y2j). The terminology "nominal propagation direction" implies that small tilts or beam spreading around the z direction are supported by the LightLike propagation machinery: i.e., LightLike makes paraxial approximations. LightLike also contains special provisions for modeling the paraxial region of point-source and rough-reflector optical fields, which would normally spread far outside the paraxial regime.
The optical-frequency factor in (Eq. 1), exp(-iwt), is completely ignored in the LightLike propagation modules. However, in the U1,2(x,y) expressions manipulated by LightLike, there is an additional, slowly-varying time dependence that is not contained in the fundamental representation of (Eq. 1). That degree of freedom is that theU1,2(x,y) fields can evolve temporally (but very slowly compared to wt), in accordance with transverse motion of turbulence screens, sources and sensors, and in accordance with the time-of-flight delay (z2-z1)/c. The propagator operation that creates U2(x,y) from U1(x,y) is itself unaware of any time tags, but transverse motions that occurs between sensor exposures, or during time of flight lags between phase screens, will cause a propagated output field to interact with a different portion of a receiver aperture, a phase screen, or whatever is acting at the z2 end. Likewise, the time at which a sensor receives a certain wavefront lags by the appropriate time-of-flight the time at which this wavefront was initiated at some source. Such lags can be vital to the correct modeling of wavefront dynamic control systems, and a consistent accounting of such lags is a strength of the internal LightLike machinery.
The field U1's monochromatic wavelength, l, is specified and used by the propagator formulas to determine diffractive effects. However, LightLike propagators always ignore the absolute overall phase factor, exp[ ik·(z2-z1)] = exp[ ik Dz ]. In the vast majority of LightLike applications, this overall phase is immaterial. If a user's application really requires a specific absolute fringe position at a specific time, an extra LightLike component can be inserted in the system model to enforce that.
In the initial paragraph, we stated that LightLike's propagators work, strictly speaking, with monochromatic fields. LightLike can treat the propagation of multiple discrete wavelengths and, to various levels of approximation, the propagation of beams whose optical spectrum has finite (continuous) width. The subsection on "Non-zero optical bandwidth", located later in the present "Theoretical background" section, outlines some general concepts and procedures that allow LightLike to be applied to fields that are not strictly monochromatic.
The degree to which finite optical bandwidth is supported, as well as the limitations of the scalar, paraxial approximations are complex subjects which are not fully explored in this User Guide. The LightLike limitations are due to analytical approximations in the fundamental formulas, as well as to practical sampling limitations in the numerical discrete spatial meshes and time steps. By scanning the contents of the User Guide, readers will find other sections that also contain information pertinent to these issues. But, to a large extent, LightLike users must take the description of the wave propagation and sensing methods given in this Guide, and then apply their own physics understanding to determine whether a LightLike model can accurately represent a problem of interest. Sometimes, a bit of specially-directed numerical experimentation will be helpful. Also, consultation with TimeLike Systems is available for general help on such questions.
Excellent general references for the underlying theory of scalar, paraxial, diffractive propagation are
(1) Goodman, Introduction to Fourier Optics, McGraw-Hill, 1968
(2) Saleh and Teich, Fundamentals of Photonics, Wiley, 1991.
Fresnel propagation
Propagation in the Fresnel regime between planes z1 and z2 can be expressed in the space domain or the spatial-frequency domain. LightLike's core numerical propagator works in the spatial-frequency domain. This fundamental propagator formula, to be found in standard texts, is
(Eq. 3): 
The vector 
denotes the x and y components of spatial frequency (cycles/m), and the overbar notation is used as a shorthand for the (-i) Fourier transform. In words, this propagator acts in three stages: (i) compute the Fourier transform of the space-domain complex field at z1, (ii) multiply by a quadratic-phase distance-propagation factor in the frequency domain, (iii) compute the inverse Fourier transform to obtain the space-domain complex field at z2.
For numerical propagation, LightLike uses a modification of this formula wherein a "reference curvature" phasor is factored off from U. That is, we define the related quantity V, where
(Eq. 4)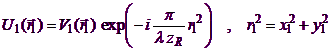 
and where zR is the "reference focus" distance (directed). (zR may be set to infinity, in which case V=U). Substituting (Eq. 4) into (Eq. 3) and regrouping terms yields the propagator formula
(Eq. 5)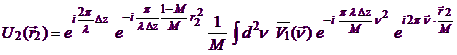 
where the "magnification" factor M = (zR - Dz) / zR = 1 - (Dz / zR). M may be less than or greater than 1, depending on the sign of zR. When M=1, (Eq. 5) reduces to the original (Eq. 3). The following figure shows whyM is called the "magnification".
The motivation for introducing the reference curvature, or equivalently M, is that in some applications the physical beam cross-section converges or diverges greatly. In such cases, we desire the NxN points of the discrete propagation mesh to span a much smaller or much larger transverse distance at z2 than at z1. If the propagator Eq. (5), with a specified M factor, is evaluated using the Discrete Fourier Transform (DFT), then the transverse space mesh is automatically compressed or stretched by the factor M. This is a natural consequence of the two DFTs in Eq (5), as the following argument shows. The first DFT, i.e., the computation of V1(bar), yields Fourier transform values on a frequency mesh of spacing Du = 1/(NDx1), and similarly for y. Next, the quadratic phase factor containing n2 is simply evaluated on that frequency mesh. Then, when another DFT is used to compute the final inverse transform, we obtain field values on the space mesh (Dx2/M) = 1/(NDu) = Dx1 , or Dx2 = MDx1.
The logic in the above paragraph is predicated on the space-frequency mesh constraints of the Discrete Fourier Transform. The specific computational algorithm used to evaluate DFTs in LightLike is the so-called Fast Fourier Transform (FFT).
Specifying the reference focus in LightLike components
The reference curvature factor, or equivalently the mesh magnification factor M, is specified in LightLike propagator components via the reference focus distance (directed) zR. For example, the key PropagationController or AtmoPath components contain parameters named xReferenceFocus andyReferenceFocus. Typically, one would set the two to the same value, but LightLike allows separate Mx andMy specifications in case of highly asymmetric problems. To use M=1, x{y}ReferenceFocus should be set to 0.0. The value 0.0 is a flag here that is interpreted as infinity focus, and this is always the default value in the LightLike propagator components.
We emphasize that many (perhaps most) LightLike applications can use the M=1 specification. Particularly if we propagate a beam in the atmosphere for a few hundred meters or kilometers or more (depending on the aperture size), there is no possibility of a greatly reduced focal spot. In many such cases, there is no need to deviate from an M=1 mesh. Additionally, there are other factors besides diffraction that need to be considered to determine the mesh sample spacing. For example, suppose we have a beam that is diverging, but is propagating through significant turbulence along the whole path. In that case, we probably want to keep the mesh spacing constant as we propagate from turbulence screen to screen. .
LightLike nomenclature: "planar reference wave" and "spherical reference wave":
The M=1 case is often referred to in LightLike documentation as the "planar reference wave" case, or sometimes as the "plane-wave" propagator case. The latter name may be misleading, in the sense that there is no implication that the full wavefront is planar anywhere.
Any M≠1 case is often referred to in LightLike documentation as the "spherical reference wave" case, or sometimes as the "spherical-wave" propagator case.
Note that zR could be the actual best-fit curvature radius of U1, but that match is not necessary. The choice of zRis arbitrary, and can be used to set the grid magnification M as desired.
Fraunhofer propagation
Components like Camera or HartmannWfsDft propagate an incident complex field U1 to the focal plane of an assumed lens of focal length f. The propagation formula used in these cases is the space-domain Fraunhofer-regime formula
(Eq. 6):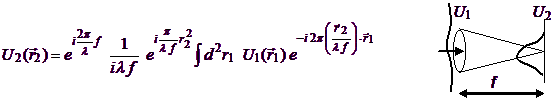 
As in the Fresnel case, the exp(ikf) factor is neglected. The DFT (implemented with the FFT) is again used to numerically evaluate the Fourier transform in (Eq. 6); the implications for the space mesh on which U2 appears are different than for the Fresnel propagator discussed previously. These mesh consequences and choices are discussed in the User Guide sections devoted to the camera sensor and the wavefront sensor.
Overall tilt and optical propagation
In a previous User Guide section, we discussed how overall tilts are typically modeled in LightLike. We explained there that large tilts introduced by tilt modules and sensor-source relative displacements are generally tracked separately by LightLike, and not incorporated into the propagating U(x,y) as a tilt phasor factor. This is done to avoid overly stressing sampling requirements in the numerical propagators. At a sensor, the separately-tracked tilt is finally inserted into the field or irradiance map by using the shift-invariance properties of the propagator.
Multi-frequency propagation and non-zero optical bandwidth
First, let us emphasize that any number of monochromatic beams of arbitrarily separated wavelengths can be propagated in a single LightLike system and run. To give a physical example of interest in adaptive optics: it is a simple matter (in terms of the multi-wavelength specifications) to study the performance degradation when a different wavelength is used for wavefront sensing than is used for the science imaging or laser beam projection. When propagating beams of different wavelengths, key questions are whether these beams interact at all, and if so, whether they add coherently or incoherently at a sensor. The answer depends (i) on whether a sensor is allowed to see multiple beams, and (ii) on the LightLike rules built into the sensor module.
LightLike has been validly used for many situations which go well beyond the strictly monochromatic regime. Depending on the problem, different approaches and justifications are used. Without going into details, we list a few concepts and procedures applicable to non-monochromatic cases:
(1) Accept a completely monochromatic model, realizing that many turbulence and diffraction effects do not change that rapidly with wavelength. This is completely satisfactory for many narrow-band propagation problems.
(2) Model a finite-bandwidth beam as a superposition of discrete-wavelength, closely-spaced, but incoherent monochromatic beams.
(3) Explicitly introduce a slowly-varying envelope function to rigorously model either a finite optical bandwidth, or the dynamic interference between closely-spaced discrete frequencies.
(4) Model an extended incoherent source plane in terms of many spatially-separated point sources, whose intensity maps will be added incoherently at a sensor.
(5) Combine a monochromatic LightLike source with specialized LightLike rough-reflector models. Several reflector models in LightLike contain features that mock up a finite bandwidth of the illuminating source, to various levels of fidelity. (I.e., some rough-reflector models in LightLike act as specialized "secondary" sources).