The LightLike library contains three basic rough-reflector modules. These are CoherentTarget, IncoherentReflector, or PartiallyCoherentReflector. By "rough reflector" we mean optically-rough in the sense that surface micro-roughness is large compared to one wavelength. We use the term "reflection" in a generic sense here: the modules could also be used to model an equivalent transmissive system, such as a ground-glass plate. In addition to the basic three systems, there are additional library systems built from these three, such as IncoherentDisk, CoherentRectangle, and IncoherentSource: these additional systems constitute various special cases or slight elaborations of the basic three. As implied by the names of the latter systems, the rough-"reflector" modules could also be used to model extended sources of various kinds, where the reflection of incident light is simply a simulation trick for modeling emission in the physical system.
The LightLike components named above make reference to various coherence states (coherent, incoherent, partially coherent). This signifies that the rough-reflector modules include features that simulate, with varying degrees of fidelity, the effect of non-zero optical bandwidths. We should emphasize that the use of these features is not the only way to model non-zero optical bandwidth in LightLike: an overview of methods is given elsewhere in the User Guide.
The rough-reflector modules can be found in the sub-library of the LightLike called Sources. The reason for this association with sources is that, at the LightLike code level, the rough reflectors are implemented as a combination of a LightLike sensor and a LightLike source that generates the reflected (scattered) wave.
The physical models used in all the rough-reflector modules treat the optically-rough limit, i.e., surface micro-roughness large compared to one wavelength. The difference between the three fundamental modules is that they apply to different levels of temporal coherence of the incident light. CoherentTarget applies to the case where the coherence length of the illumination is long compared to the macro-depth of the target. This is the typical textbook laser-speckle case. IncoherentReflector is a relatively crude extension of the CoherentTarget concept that attempts to treat the limit where coherence length of the illumination is short compared to the macro-depth of the target. PartiallyCoherentReflector is a more physically-based model than IncoherentReflector, and carefully treats the intermediate case where coherence length of the illumination is of the same order as the macro-depth of the target. The key additional phenomenon that we model using IncoherentReflector and PartiallyCoherentReflector is the reduction in speckle contrast due to the finite temporal coherence of the illumination.
CoherentTarget
Basics
CoherentTarget is the simplest of the three basic modules. CoherentTarget applies to the case where the coherence length of the illumination is long compared to the macro-depth of the target. This is the fundamental laser-speckle case treated in every modern-optics textbook.
When an optically rough surface is illuminated by a monochromatic beam, the phase differences across a surface of the exiting wave are still constant in time, although the phasefront becomes extremely rough. The assumption used in the basic theoretical treatment is that, in an exit plane after reflection, the phase of the exiting beam is uncorrelated from point to point, and has a standard deviation much greater than 1 wave (or equivalently, the mod-2p phase is practically uniformly distributed over 2p radians). In accordance with this concept, CoherentTarget works by initially defining a spatially uncorrelated exit phase map, and propagating the resulting beam though the remainder of the LightLike system. In addition to internally generating the random-phase map, f(x,y), CoherentTarget allows the user to specify an intensity reflectance map, R(x,y), where (x,y) is transverse to the nominal propagation direction. R(x,y) allows the user to specify a target of arbitrary shape and non-uniform reflectance strength across the target. .
Some details
In the real world, the roughness of the phasefront causes the reflected light to be scattered over a very broad angular range. Treating this in simulation involves some subtleties. As in the case of a point source, it is not possible to model the entire speckle wavefront, but neither is it necessary. We are generally only interested in that part of the light that might eventually enter the aperture of the optical system in question, and so we can use techniques similar to those we use in modeling point sources. To be specific, the default speckle modeling approach is to begin by generating a wavefront where the amplitude is computed from the amplitude of the incident wavefront, the intensity-reflectance map of the rough reflector, and a phase that is spatially uncorrelated and uniformly distributed on (-p to p). We then perform a vacuum propagation to the aperture plane, and multiply the field by a weighting function of unity over a circular region somewhat larger than the aperture, then dropping smoothly to zero. Finally, we do a second vacuum propagation back to the source plane, which yields the initial speckle field we will use to propagate back through turbulence.
The net effect of this technique is similar to spatial filtering, smoothing the speckle phasefront enough to limit the angular spread of the light, but our approach offers a useful advantage: regardless of the size and shape of the incoherent reflector, from each point on the reflector we capture all the light headed toward the system aperture, and only that light, automatically. Using spatial filtering, light from every point on the reflector leaves with the same angular spread, and it is incumbent on the user to ensure that the spread is great enough that the light from every point fully illuminates the aperture. This creates an opportunity for error, and for large reflectors it can make it necessary to use larger propagation meshes than would otherwise be needed, because of the larger angular spread required to ensure full illumination of the aperture.
To specify speckle modeling parameters, you will need to use a PropagationController, as described in choosing parameter settings for modeling optical propagation. To use the default modeling approach, set the parameter speckleModel to DEFAULT_SM, as shown, and use superApDiameter and edgeSigma to specify the aperture plane weighting function; see the recommendations given in how point sources are modeled.
To use the more conventional approach of starting with a delta-correlated speckle field, then using spatial filtering, set speckleModel to DELTA_CORRELATED_SM, and then specify the spatial filter as described in how to use spatial filters and absorbing boundaries.
IncoherentReflector
Suppose we illuminate an optically rough surface with light whose temporal coherence length is short relative to the macro-depth of the target surface. By macro-depth we mean the changing distance between target surface and receiver, due to target surface tilt or 3D shape. In this situation, when the distance differences between a receiver-plane point and different target points exceed the light's coherence length, optical interference will no longer be possible at typical detector response times. Therefore, the contrast of the speckle pattern can be greatly reduced.
The IncoherentReflector module is a relatively crude attempt to model reduction in rough-surface speckle contrast, while still allowing the propagated light to be influenced by turbulence and other factors along the propagation path. IncoherentReflector causes the following calculations:
(i) generation of "nWaves" independent rough-surface phase realizations, each on the principles of CoherentReflector (the value nWaves is user-specified)
(ii) propagation of each of the nWaves reflected waves through the remainder of the LightLike system
(iii) averaging at any sensor of the nWaves speckle irradiance patterns.
Note that the nWaves parameter is the only degree of freedom in the model (as far as the partial coherence aspect is concerned).
As was the case in CoherentTarget, the IncoherentReflector allows the user to specify an intensity reflectance map, R(x,y), where (x,y) is transverse to the nominal propagation direction. R(x,y) allows the user to specify a target of arbitrary shape and non-uniform reflectance strength across the target.
The conceptual weakness of the IncoherentReflector model is that there is no general quantitative formula that accurately relates the simple nWaves parameter to the speckle reduction details that correspond to a general illumination scenario.
PartiallyCoherentReflector
In contrast to IncoherentReflector, the PartiallyCoherentReflector model contains a much more precise mathematical model of the interaction between light of specified temporal coherence and a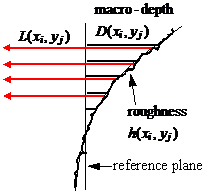
rough reflector with specified macro-depth. As in the simpler rough reflectors, the model still generates a spatially-uncorrelated phase associated with the surface roughness h(x,y). However, a user-specified macro-depth profile, D(x,y), is also entered into the model, along with a numerical value of the illumination temporal coherence length,lc. LightLike begins by generating nWaves statistical realizations of a slowly-varying envelope (SVE) phasor consistent with lc. For a given SVE realization, a reflected exit wave in the reference plane is formed from the incident complex field in the reference plane by folding in the geometric OPDs corresponding to h as well as D. After this, the exit complex field is propagated by the usual LightLike means through the remainder of the LightLike system. This sequence is carried out for each of the nWaves statistical realizations of the SVE phasor, and at any sensor the resulting nWaves irradiance maps are averaged. This full sequence of operations explicitly represents the averaging reported by any square-law detector over the response time of the detector (assumed long compared to the coherence time of the radiation). The main "loose end" in the model is the number nWaves required to achieve a reliable estimate of the average.
Users who wish a more detailed discussion of the PartiallyCoherentReflector model and input parameters, along with a validation study that compares numerical performance with a theoretical result, should consult a section an auxiliary document.