There are two (linked) aspects of sign and phasor conventions that may be important to the user:
(1) For LightLike input purposes, the most important issue is whether positive or negative signs of tilt parameters cause beams to be deflected up or down, and whether positive or negative signs of focus parameters cause beams to converge or diverge. This is defined in the first section below ("sign conventions").
(2) A secondary issue is how signs are defined in phasor expressions that mathematically represent tilt, focus, or general transverse OPD. When defining LightLike inputs and parameters, the user does not usually need to know these details. However, if recorded outputs of the SimpleFieldSensor module are used to inspect complex fields, then the user may wish to know all the sign conventions used by LightLike for the phasors. This is discussed in the second section below ("phasor conventions").
In reading the documentation on sign and phase conventions, we recommend that the user first focus on the essential issue number (1), and just refer back to the explanations of issue (2) as needed.
Sign conventions for tilt, focus, and general OPD
Tilt
LightLike has several modules (notably Tilt, Slew and BeamSteeringMirror) that apply a tilt-angle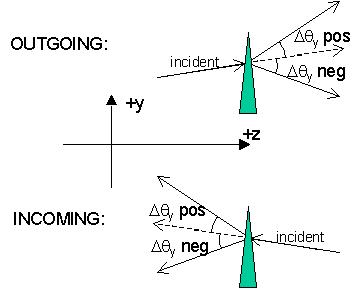
increment to an incident wave. In these modules, one inputs a tilt angle (Δθx,Δθy), in units of radians of angle. The sign convention for tilt angle in LightLike is motivated by the geometric picture of beam deflection as shown in the following figure. The picture is drawn in unfolded form as if deflection is effected by a prism, in accordance with LightLike's "incident-transmitted" treatment of waves as discussed above.
The diagram shows the meaning of the tilt sign when combined with the two possible z-directions of propagation. The rule is:
(a) Positive Δθy means that the beam is steered towards positive y.
(b) Negative Δθy means that the beam is steered towards negative y.
(c) Statements (a) and (b) hold for both outgoing and incoming incident waves. This is consistent with the fact that, if outgoing and incoming beams are affected by the same element, then they are both steered toward -y or both toward +y. The interpretation of Δθx of course follows the identical pattern.
The representation of tilt in LightLike has a twist that users must understand to work effectively. Tilts applied by modules like Tilt and BeamSteeringMirror can either be
(1) carried separately in computation from the residual complex field, or
(2) incorporated into the complex field, by multiplying the incident field by a phasor factor.
At present, we only alert the reader to the existence of this feature: the reasons for and various implications of this dual representation are quite important, and are discussed more fully in a later section that discusses how tilt is modeled internally.
Focus
LightLike's Focus module applies a quadratic phase increment (a focus or defocus) to an incident wave. The Focus module requires a signed input value called "focusDistance", for which we here used the symbol f. The LightLike sign convention for focusDistance is:
(a) Positive f causes the incident wave to become more convergent.
(b) Negative f causes the incident wave to become more divergent.
(c) Statements (a) and (b) hold for both outgoing and incoming incident waves.
The sign convention for f corresponds to what is called "power" in first-order optical design: positive power or f tends to converge an incident wave, and negative power or f tends to diverge an incident wave, regardless of the propagation direction.
Phasor conventions for tilt, focus, and general OPD
As noted in the introduction to the previous section on signs, LightLike's internal phasor conventions are only significant to users when they wish to inspect the complex field output of the SimpleFieldSensor module.
Tilt
If a tilt-generating module is instructed to "put the tilt into the complex field" (see the section on how tilt is modeled), then the complex field incident on the module is multiplied by the phasor
OUTGOING waves: exp[ +i(2π/λ)(Δθx x + Δθy y) ]
INCOMING waves: exp[ -i(2π/λ)(Δθx x + Dqy y) ] ,
where we recall from above that Δθx and Δθy may themselves be positive or negative.
The critical reader may question the consistency of LightLike's tilt-angle phasor convention. For the purpose of background understanding, consider the following. Suppose we write the fundamental vectorial representation of a plane wave phasor using the "-iωt" convention:
exp[ i(k*r - ωt) ] = exp[ i(kxx + kyy + kzz - ωt) ] ,
where the bold quantities indicate vectors, k is the wave vector and w is the optical angular frequency. The relevant point here is this: as t advances, positive kz forces a constant-phase surface to move toward +z (what we call "outgoing"), while negative kz forces a constant-phase surface to move toward -z ("incoming"). Likewise, regardless of the sign of kz, the sign of ky determines whether the wave moves upward or downward along y, and similarly for x. Now it would be logical to define the tilt angle via the relation ky = (2π/λ)(Δθy), that is, to assign the same sign to ky and to Δθy. However, we see that the LightLike tilt-phasor convention violates this relation, since an extra (+/-) factor has been inserted depending on (outgoing/incoming) status. The LightLike convention evidently conflicts with the exp[i(k*r - ωt)] representation; in fact the LightLike convention can be viewed as switching between "-iωt" and "+iωt" conventions depending on whether outgoing or incoming waves are being represented. Nevertheless, no contradictions arise within the allowed operations of LightLike. Certain signs in the propagators are defined consistently with the wave phasor signs. Additionally, a critical fact is that LightLike's splitter/combiner modules never allow outgoing and incoming waves to be combined for possible complex superposition on a field sensor. It is only possible to compute the complex superposition of several outgoing or of several incoming waves. Under this restriction, the LightLike conventions will give correct interference results.
Focus
LightLike's Focus module applies a quadratic phase increment (a focus or defocus) to an incident wave. The complex field incident on Focus is multiplied by the phasor
OUTGOING waves: exp[ - i(2π/λ) (x2 + y2)/(2f) ]
INCOMING waves: exp[ +i(2π/λ) (x2 + y2)/(2f) ] ,
where f is a signed input value called "focusDistance" in the Focus module. As discussed in the previous section, the sign convention for f is:
positive f causes the incident wave to become more convergent,
negative f causes the incident wave to become more divergent,
where this holds for both outgoing and incoming incident waves.
LightLike's focus phasor sign convention has a consistency issue analogous to that discussed in the preceding tilt section. But as outlined there, no contradictions arise within the presently allowed operations of LightLike.
General OPD
A general, transversely-varying phase function can be represented by
ϕ(x,y) or (2π/λ)d(x,y)
where the transverse OPD function is in radians of phase (f) or in meters (d). LightLike has several modules (e.g., OpdMap and FixedOpdMap) which allow the multiplication of an incident wave (complex field) by a phasor created from a discrete input array d(xi, yj). The phasor factor is defined as
OUTGOING waves: exp[ +i(2π/λ)d(x,y) ]
INCOMING waves: exp[ - i(2π/λ)d(x,y) ] .
For example, in light of the previous focus discussion, an input { d(xi, yj) = - |a| yj2 } should generate a phasor factor that adds a positive-f (converging) cylinder focus factor to both outgoing and incoming waves.
Absolute phase
LightLike does not keep track of absolute phase in its propagation modules. That is, a complete Fresnel propagation operator from plane 1 to plane 2 includes a factor exp[i(2π/λ)Δz21], but this factor is omitted in LightLike propagations.