In wave optics simulation, optical wavefronts are represented using two-dimensional rectangular complex meshes. In order to obtain correct simulation results, it is important to choose mesh spacings small enough to ensure that the variations in the wavefront will be properly sampled, and to choose the mesh dimensions large enough to capture the region of interest, and also to ensure that wrap-around effects (a well-known artifact of FFT propagation) will not impinge on the region of interest when we propagate the wavefront from one plane to another.
Because the meshes used are necessarily finite in extent, we can only model light sources and receivers which are likewise finite in extent. Similarly, because the mesh spacings are finite, we can only model wavefronts which do not vary too rapidly; that is, the angular (spatial frequency) spectrum of the wavefront must be bandlimited, and the band limit must be less than or equal to the Nyquist frequency: |θ| ≤ λ/(2*δ). To be precise, the above inequality applies exactly if and only if the angular spectrum is computed with respect to reference wavefront to be used in propagation. The reference wavefront is the surface, typically planar or spherical, which projects each mesh point at the source plane with a corresponding point on the receiver plane. (In the most general case the reference wavefront is the product of two cylinder wavefronts, one in x and one in y, which need not have the same curvature.)
The fact that we can only model bandlimited wavefronts is less of a limitation than it might at first appear, because the fact that both the source and receiver must be finite in size and separated by some distance implies that the light reaching the receiver will always be bandlimited, whether the light leaving the source is or is not. Light leaving the source at angles outside the range spanned by the rays connecting the source and receiver apertures will never reach the receiver, and therefore we don’t need to model it. To correctly model a source that radiates over wide angles, one needs to determine what its spectrum looks like across the angular range that can affect the field seen at the receiver; all the rest of the angular spectrum can then be discarded, either analytically, or by applying a spatial filter.
In the following, we shall describe how to choose mesh spacings and mesh dimensions which will yield correct simulation results for any coherent light source and receiver, provided both are of finite extent, and separated by some appreciable distance (long enough that small angle approximations are valid). First we will consider the case of propagation through vacuum, and then we will show how those results can be generalized for the case of propagation through turbulence. Throughout the discussion we will work with only one transverse dimension, which can be thought of as either x or y, where by convention the propagation direction is assumed to be along the z axis. All of the same considerations and inequalities apply to the mesh spacings and dimensions in both x and y, and furthermore they are mutually independent, so the mesh spacings and dimensions in x and y can be chosen independently.
1. Propagation through vacuum
In the case of propagation through vacuum, the requirements pertaining to the mesh spacings and mesh dimensions can be computed directly from the basic geometry of the problem. In one dimension, the basic geometry of any propagation scenario can be defined in terms of the following four parameters (shown in Figure 1):
λ the wavelength (m)
Z the propagation distance, from source to receiver (m)
D1 the spatial extent of the source transverse to the propagation direction (m)
D2 the spatial extent of the receiver transverse to the propagation direction (m)
Given λ, Z, D1, and D2 we wish to choose the mesh spacings at the two planes, δ1 and δ2, and the number of mesh samples (a.k.a. the mesh dimension), n, so as to obtain the correct field over the region of interest in the receiver plane. In general, the correct field will be obtained if and only if we choose δ1, δ2, and n so as to satisfy the following two inequalities (derived later in this memo in the section entitled “Derivations”):
δ1*D2 + δ2*D1 ≤ λ*Z (1)
n ≥ D1/(2δ1)+ D2/(2δ2) + λZ /(2δ1δ2) (2)
From the first inequality we can obtain strict upper bounds for each of the two mesh spacings:
δ1 < λ*Z/D2 (3)
δ2 < λ*Z/D1 (4)
Note, however, that as soon as one of the spacing has been chosen, that further constrains our choice for the second spacing:
Given δ1, δ2 ≤ (λ*Z - δ1*D2)/ D1 (5)
Given δ2, δ1 ≤ (λ*Z - δ2*D1)/ D2 (6)
Note also that if we choose either mesh spacing very close to its upper bound, the other mesh spacing is then driven very close to zero, and as a consequence the number of mesh points required, n, becomes very large. To minimize n, the mesh spacings should be chosen as follows:
δ1 = λ*Z/(2D2) (7)
δ2 = λ*Z/(2D1) (8)
With those mesh spacings, the inequality for n reduces to this:
n ≥ 4D1D2 / (λZ) (9)
Sometimes it is useful or desirable to keep the mesh spacings at the two planes equal; this is sometimes refrerred to as plane wave propagation. For this case the inequalities take the following form:
δ1 = δ2 = δ ≤ λ*Z / (D2 +D1) (10)
n ≥ (D1+D2)/(2δ) + λZ /(2δ2) (11)
Note that if one reduces the mesh spacings, the minimum number of mesh points required increases, and the dependence is not linear, but quadratic.
2. Propagation through turbulence
In the case of propagation through vacuum, in addition to the considerations described in the previous section, we must also take into account the optical effects of turbulence. Fortunately, this turns out to be relatively easy to do: we can use all of the same inequalities given in the previous section, but in place of the actual physical extents of the source and receiver (D1 and D2), we simply substitute the apparent extent of the blurred image of each as seen from the other (D1’ and D2’). The blurred image of the source (receiver) as seen by the receiver (source) is broader on average than the pristine image by the width of a blur function, approximately gaussian, which varies inversely with the spherical wave coherence diameter computed from the source (receiver) to the receiver (source). Fried’s coherence length (r0) is a good representation of the spatial extent of the turbulence. Since the turbulence can be different at the source and receiver, r01 and r02 will be used to indicate the coherence length at the source and receiver respectively. If we assume a simplified model of the turbulence as diffraction from the first order of a grating with an effective spatial frequency of 1/r0, the diffraction angle is given by θ ≈ sin(θ) = λ/r0. Thus, the blurring can be modeled as an increase in the aperture diameter at the source and receiver of cturb*λ*z/r0, where cturb is a factor used to indicate the sensitivity of the model to the turbulence. Choosing cturb greater than 4.0 is fairly conservative, but for some application values as low as 2.0 or as high as 8.0 are needed. This leads us to the following:
D1’ = D1 + cturb*λ*z/r01 (12)
D2’ = D2 + cturb*λ*z/r02 (13)
δ1*D2’ + δ2*D1’ ≤ λ*z (14)
δ1 = λz/(2D2’) (15)
δ2 = λz/(2D1’) (16)
n ≥ D1’/(2δ1) + D2’/(2δ2) + λ*z / (2δ1δ2) (17)
To see why the appropriate values for cturb typically fall in the neighborhood of 2.0 to 4.0, we need to look at the point spread function associated with propagation through turbulence, or, to be more precise, we need to look at what fraction of the total energy is retained (and what fraction is discarded) when we truncate the turbulence PSF as a particular angle, as a function of that angle. The encircled energy curve is shown in Figure 1.
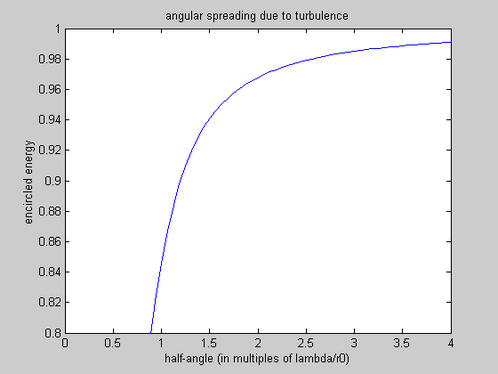
Figure 1. Angular spreading due to propagation through turbulence.
3. Examples
Suppose the basic geometry parameters are as follows:
λ 1.0e-6 m
Z 1.0e5 m
D1(vacuum) 1.5 m
D2(vacuum) 3.0 m
Reference wave Planar
a.Propagation through vacuum (Fried’s Coherence Length = r01 = r02 = infinity), picking spacings so as to minimize n.
δ1 = λ*Z/(2D2) = 1.0e-6*1.0e5/(2*3.0) = 0.0167 m
δ2 = λ*Z/(2D1) = 1.0e-6*1.0e5/(2*1.5) = 0.0333 m
n ≥ 4D1D2 / (λZ) = 4*1.5*3.0/(1.0e-6*1.0e5) = 180
b.Propagation through vacuum (r01 = r02 = infinity), plane wave propagation.
δ1 = δ2 = δ ≤ λ*Z / (D2+D1) = 1.0e-6*1.0e5/(1.5+3.0)= 0.0222 m
If we choose δ = 0.0222 m,
n ≥ (D1+D2)/(2δ) + λZ /(2δ2) = 202.8
If we choose δ = 0.02 m,
n ≥ (D1+D2)/(2δ) + λZ /(2δ2) = 237.5
c.Propagation through turbulence (r01 = r02 = 0.2 m, c_turb=4.0), picking spacings so as to minimize n.
D1 = D1 (vacuum) + λZ / r02 = 1.5 + 4.0*1.0e-6*1.0e5/(0.2) = 3.5 m
D2 = D2 (vacuum) + λZ / r01 = 3.0 + 4.0*1.0e-6*1.0e5/(0.2) = 5.0 m
δ1 = λ*Z/(2D2) = 1.0e-6*1.0e5/(2*5.0) = 0.010 m
δ2 = λ*Z/(2D1) = 1.0e-6*1.0e5/(2*3.5) = 0.0143 m
n ≥ 4D1D2 / (λZ) = 4*3.5*5.0/(1.0e-6*1.0e5) = 700
d.Propagation through turbulence (r01 = r02 = 0.2 m, c_turb=4.0), plane wave propagation.
D1 = D1 (vacuum) + λZ / r02 = 1.5 + 4.0*1.0e-6*1.0e5/(0.2) = 3.5 m
D2 = D2 (vacuum) + λZ / r01 = 3.0 + 4.0*1.0e-6*1.0e5/(0.2) = 5.0 m
δ1 = δ2 = δ ≤ λ*Z / (D2+D1)= 1.0e-6*1.0e5/(3.5+5.0) = 0.0118 m
If we choose δ = 0.0118,
n ≥ (D1+D2)/(2δ) + λZ /(2δ2) = 719.3
If we choose δ = 0.01,
n ≥ (D1+D2)/(2δ) + λZ /(2δ2) = 925
It is important to remember that simulation execution time scales roughly n2log n, and that minimum n goes up quadratically, with any decrease in the mesh spacings below the values that minimize n, so decreasing the mesh spacing significantly can be very expensive in terms of execution time.
4. Derivations
All of the results cited in the previous sections follow from the two inequalities stated at the beginning of Section 1:
δ1*D2 + δ2*D1 ≤ λ*Z (18)
n ≥ D1/(2δ1)+ D2/(2δ2) + λZ /(2δ1δ2) (19)
The first inequality follows from the Nyquist sampling requirement (|θ| ≤ λ/(2*δ)), which applies exactly to the angular spectrum is of the wavefront computed with respect to reference wavefront to be used in propagation, and the angular spectrum of the light reaching the receiver, which is constrained by the finite sizes of the source and receiver and the distance by which they are separated. For most Fourier propagation, the reference wavefront is usually assumed to be planar, but can in general be any surface comprised of spherical curvature in x and y. Thus, the following derivation will assume only a spherical reference wavefront.
The maximum angle that we need to satisfy the sampling requirement always occurs for a ray connecting one edge of the source aperture with the opposite edge of the receiver aperture, but the value of the angle depends on our choice of reference wave because the maximum angle is measured relative to a line normal to the reference wave. If the reference wave is chosen so as to project the center of region of interest at the source plane onto the center of the region of interest at the source plane, then the only remaining degree of freedom is its curvature, which determines the ratio of the mesh spacings at the two planes, δ1 and δ2.
For the vacuum case, using small angle approximations (a.k.a. paraxial ray approximations) and the variables defined in Figure 2, an expression for the angle between the z axis and the line connecting the lower (-D1/2) edge of the source aperture, which we will take to be at z=0, to the upper (+D2/2) edge of the receiver aperture, at z=Z is given by
Source plane point: (-D1/2, z=0)
Receiver plane point: (D2/2, z=Z)
θedge-to-edge = (D2/2 + D1/2) / Z = (D2+D1) / (2Z) (20)
Next, we need an expression for the angle of the angle between the z axis and the normal to the reference wavefront at the lower edge of the source plane.
Source plane point: (-D1/2, z=0)
Receiver plane point: (-D1/2 *(δ2/δ1), z=Z)
θreference_normal = (-D1/2 *(δ2/δ1) + D1/2)/ Z = (D1*(1 - δ2/δ1 )) / (2Z) (21)
The maximum angles we need to sample at the source plane is just the the difference between the above two angles:
θmax_1 = (D2+D1) / (2Z) - (D1*(1 - δ2/δ1 )) / (2Z) = (D2 + D1*δ2/δ1 ) / (2Z) (22)
Figure 3 shows the two different maximum angles, θmax_1 and θmax_2, for light propagating from plane 1 to 2 for the diverging and converging cases respectively.
Applying the Nyquist sampling requirement at the source plane, we obtain
θmax_1 ≤ λ/(2*δ1) (23)
Combining our expression for θmax_1 and the Nyquist sampling requirement ensures that the mesh is large enough such that that energy will not reach the edge of the mesh and create deleterious “wrap-around” (i.e. reappear at the opposite side of the mesh) and affect the field in the region of interest at the receiver plane and results in the inequality,
(D2 + D1*δ2/δ1 ) / (2Z) ≤ λ/(2*δ1) (24)
δ1*D2 + δ2*D1 ≤ λ*Z (25)
Note that even though we applied the Nyquist sampling requirement only at the source plane, in the resulting inequality the source plane and receiver plane quantities play interchangeable roles. The same expression can also be obtained by applying the Nyquist requirement at the receiver plane.
Now the inequality related to the number of mesh points required can be derived based on the knowledge of mesh spacings, δ2 and δ1 , and the desire to avoid wrap-around. In the absence of any wraparound, the size of the region at the receiver plane illuminated by the light from the source, shown in Figure 4, would be the equal to projection of the source aperture along the normals to the reference wavefront, D1*δ2/δ1 , plus the two times the propagation distance (Z) times the largest angle representable on the source plane mesh λ/(2δ1):
Dilluminated_at_receiver = D1*δ2/δ1 + λΖ/δ1 (26)
In general, Fourier propagation can allow wraparound as long as it does not wrap enough to reach the area of interest. In order to ensure that wraparound effects will not impinge upon the region of interest, the mesh width must be greater than or or equal to the mean of the sizes of the illuminated region and the region of interest, shown in Figure 5. This results in the inequality,
Dmesh_at_receiver ≥ (Dilluminated_at_receiver + D2) / 2 = (D1*δ2/δ1 + λΖ/δ1 + D2) / 2 (27)
The minimum number of mesh points required to ensure that wraparound effects will not impinge upon the region of interest is just the minimum mesh size at the receiver divide by the mesh spacing at that plane is given by
n = Dmesh_at_receiver / δ2 ≥ (D1*δ2/δ1 + λΖ/δ1 + D2) / 2δ2 (28)
n ≥ D1/(2δ1)+ D2/(2δ2) + λZ /(2δ1δ2) (29)